Roderic Guigó, IMIM and UB, Barcelona
SEARCH BY SIGNAL
Introduction
What is a motif?
Let A={A,C,G,T} be the alphabet of the nucleotide sequences. A
motif (pattern, signal...)
is an object dennoting a set of sequences on this alphabet, either in a
deterministic or probabilistic way.
Given a sequence S and a motif m, we will say that the motif m occurs in
S if any of the sequences denoted by m occurs in S.
A Hierarchy of Motif Descriptors
Sequence motifs can be described in a wide variety of ways.
Exact Word
The description is an specific sequence in the
alphabet.
CTTAAAATAA
Consensus Sequences
The description allows for the
specification of alternative nucleotides occurring at a given position.
YTWWAAATAR (Consensus MEF2 sequence, Yu et al., 1992)
CTAAAAATAA
TTAAAAATAA
TTTAAAATAA
CTATAAATAA
TTATAAATAA
CTTAAAATAG
TTTAAAATAG
..........
Regular Expressions
The description is built on an
extension of the original alphabet. Among the new symbols of this extended
alphabet, there symbols dennoting the alternative occurence of a number of
nucleotides at a given position, and symbols denoting that a given
position may not be present.
C..?[STA]..C[STA][^P]C
2Fe-2S ferredoxin, iron-sulfur binding region signature,
PROSITE database, Bairoch, 1991)
Other examples,
DNA polymerase family B signature
EF-hand calcium-binding domain
This is an
structural motif
Position Weigth Matrices (PWMs) or Position Specific Scoring Matrices
The description includes a
weight (score, probability, likelihood) for each symbol occuring at each
position along the motif.
Follow the link for An Introduction to Position Weigth Matrices
Examples of PWMs
- A PWM for donor sites.
From a set of aligned donor sites we derive the following probability matrix
-5 -4 -3 -2 -1 +1 +2 +3 +4 +5 +6 +7 +8
A 26.0 27.7 35.1 59.6 8.7 0.0 0.0 50.7 72.1 7.0 15.8 26.6 19.7
C 25.5 29.4 34.8 13.3 2.7 0.0 0.0 2.8 7.6 4.7 17.2 21.7 29.4
G 23.8 25.3 18.5 13.2 80.9 100.0 0.0 43.9 12.2 83.1 18.8 32.7 24.5
T 24.7 17.5 11.6 13.9 7.7 0.0 100.0 2.5 8.1 5.2 48.3 18.9 26.4
C/A A G G T A A G T
which assuming nucleotide equiprobability tranforms in the following log-likelihood matrix:
-5 -4 -3 -2 -1 +1 +2 +3 +4 +5 +6 +7 +8
A 0.04 0.10 0.34 0.87 -1.05 -inf -inf 0.71 1.06 -1.27 -0.46 0.06 -0.24
C 0.02 0.16 0.33 -0.63 -2.22 -inf -inf -2.17 -1.19 -1.68 -0.38 -0.14 0.16
G -0.05 0.01 -0.30 -0.64 1.17 1.39 -inf 0.56 -0.72 1.20 -0.29 0.27 -0.02
T -0.01 -0.36 -0.77 -0.59 -1.18 -inf 1.39 -2.29 -1.13 -1.58 0.66 -0.28 0.06
The positions showing higher bias in nucleotide composition are the most informative positions.
Indeed, we can compute the information content at each position D(i), by using Shanon's formula
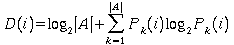
where
A is the alphabet {A, C, G, T}
|A| is the number of elements in A, (A=4)
Pk(i) is the probability of observing base k in position
i
so for a postion with nucleotide equiprobability P = 1/4, the information content is zero
D(i) = 0 = 2 + 1/4 log2(1/4)
+ 1/4 log2(1/4) + 1/4 log2(1/4) + 1/4 log2(1/4)
The information content along a sequence aligment can be nicely visualized by means of the so-called sequence logos.
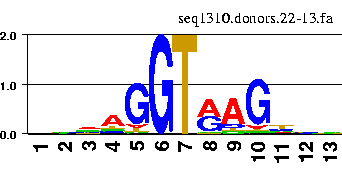 There are a number of web servers that allow to generate the logos interactively. For instance
the GENIO/logo server.
You can try with the fasta file containing the aligment of above donor sites.
There are a number of web servers that allow to generate the logos interactively. For instance
the GENIO/logo server.
You can try with the fasta file containing the aligment of above donor sites.
The Jaspar Matrices
Modelling dependencies between positions
In the case of the donor sites above, the matrix reproduces the
complement to the sequence at the 5' end of the RNA molecule in the U1
snRNP, which interacts with the pre-mRNA sequence to recognize the
donor site during the splicing process. This suggest that the
recognition of the donor site is mediated by the formation of base
pairs. The higher the complementariety between the precursor RNA
molecule at the donor site and the 5' end of the U1 snRNP, higher the stability of the interaction.
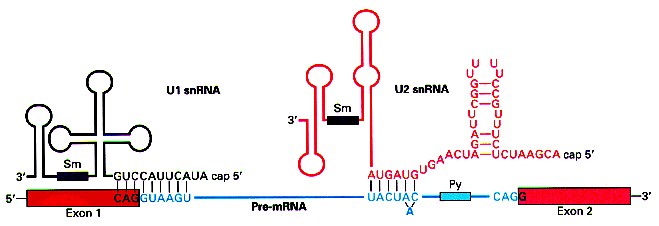
(Figure taken from http://www.orst.edu/instruction/bb331/lecture10/lecture10.html)
It is well known, however, that the staking energy
contributes to the stability of the double stranded DNA. This staking energy depends on
nearest neighbour arrengements along the DNA molecule.
Tables of staking energy are constantly being updated.
This suggest that the positions along the donor site sequence are not independent. That is, the existence of a given nucleotide at a given position may influence the probability of the nucleotides at the nearby positions.
We can test this hypothesis by estimating the conditional probabilities of each nucleotide at each position, depending on the nucleotide at the precedent position, in the set above of known donor sites.
position -3 position -2 position -1 position 1 position 2 position 3 position 4 position 5 position 6
A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T
A 29.2 31.9 25.5 13.4 62.4 9.5 15.2 12.9 7.0 1.7 86.2 5.1 0.0 0.0 100.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 65.4 9.5 13.3 11.8 6.0 3.0 87.4 3.7 19.1 15.9 39.8 25.3
C 48.6 32.5 6.2 12.7 69.2 11.6 6.4 12.8 19.1 7.1 55.2 18.5 0.0 0.0 100.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 72.7 4.7 6.7 16.0 19.5 17.8 42.8 20.0 24.8 25.2 10.6 39.4
G 38.8 36.2 17.7 7.3 62.6 15.8 12.3 9.3 12.3 2.4 79.1 6.2 0.0 0.0 100.0 0.0 0.0 0.0 0.0 100.0 0.0 0.0 0.0 0.0 82.5 5.6 9.0 2.9 6.2 4.2 86.1 3.4 15.2 17.2 15.9 51.7
T 16.4 41.3 29.5 12.9 17.7 25.6 29.5 27.2 2.9 3.3 84.4 9.4 0.0 0.0 100.0 0.0 0.0 0.0 0.0 0.0 50.8 2.8 43.8 2.5 26.9 7.5 50.7 14.9 6.1 7.9 78.7 7.2 12.5 10.7 43.4 33.5
35.1 34.8 18.5 11.6 59.6 13.3 13.2 13.9 8.7 2.7 80.9 7.7 0.0 0.0 100.0 0.0 0.0 0.0 0.0 100.0 50.7 2.8 43.9 2.5 72.1 7.6 12.2 8.1 7.0 4.7 83.1 5.2 15.8 17.2 18.8 48.3
we can use this conditional probability distribution to compute the probabilyt of a given sequence in a donor site.
The probability of sequence S=s1s2s3s4s5s6s7s8s9 in a donor site can be computed now as
P(S)=P(s1) P(s2/s1) P(s3/s2) P(s4/s3) P(s5/s4) P(s6/s5) P(s7/s6) P(s8/s7) P(s9/s8)
where P(si/sj) is the probability of nucleotide sj in position k given that nucleotides si is at position k-1.
For instance, the probability of finding sequence S=CAGGTTGGA is
P(S)= 0.35 * 0.69 * 0.55 * 1.00 * 1.00 * 0.02 * 0.51 * 0.86 * 0.15
Actually, we usually compute a log-likelihood ratio as above. Assuming for instance p(si/sj)=0.25 ---that is, that there is no dependence between positions, we obtain the following log-likelihood matrix
position -3 position -2 position -1 position 1 position 2 position 3 position 4 position 5 position 6
A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T A C G T
A 0.15 0.24 0.02 -0.62 0.91 -0.97 -0.50 -0.66 -1.28 -2.72 1.24 -1.58 -inf -inf 1.39 -inf -inf -inf -inf -inf -inf -inf -inf -inf 0.96 -0.97 -0.63 -0.75 -1.43 -2.12 1.25 -1.92 -0.27 -0.46 0.46 0.01
C 0.66 0.26 -1.40 -0.67 1.02 -0.76 -1.37 -0.67 -0.27 -1.25 0.79 -0.30 -inf -inf 1.39 -inf -inf -inf -inf -inf -inf -inf -inf -inf 1.07 -1.68 -1.32 -0.45 -0.25 -0.34 0.54 -0.22 -0.01 0.01 -0.86 0.46
G 0.44 0.37 -0.35 -1.24 0.92 -0.46 -0.71 -0.99 -0.71 -2.33 1.15 -1.40 -inf -inf 1.39 -inf -inf -inf -inf 1.39 -inf -inf -inf -inf 1.19 -1.50 -1.02 -2.16 -1.39 -1.78 1.24 -1.99 -0.50 -0.37 -0.45 0.73
T -0.42 0.50 0.16 -0.66 -0.35 0.02 0.17 0.08 -2.16 -2.03 1.22 -0.97 -inf -inf 1.39 -inf -inf -inf -inf -inf 0.71 -2.17 0.56 -2.29 0.07 -1.21 0.71 -0.52 -1.41 -1.15 1.15 -1.24 -0.69 -0.85 0.55 0.29
0.34 0.33 -0.30 -0.77 0.87 -0.63 -0.64 -0.59 -1.05 -2.22 1.17 -1.18 -inf -inf 1.39 -inf -inf -inf -inf 1.39 0.71 -2.17 0.56 -2.29 1.06 -1.19 -0.72 -1.13 -1.27 -1.68 1.20 -1.58 -0.46 -0.38 -0.29 0.66
OTHER PRACTICALS
PRACTICAL 1
PRACTICAL 2
PRACTICAL 3